Open-sourcing SymForce: Skydio's framework for writing algorithmic code

Writing code that powers robots is a complex challenge. Algorithms must meet a very high bar of robustness and performance to ship in production, leading to a slow iteration cycle that requires dedicated expertise in both research and software engineering. At Skydio, improving this iteration cycle was a crucial problem we had to solve to make our drones smarter and faster. To do this, we developed SymForce — a framework for writing algorithmic code using symbolic computation and code generation. Today, we're excited to take the next step and open-source SymForce to help accelerate innovation across robotics.
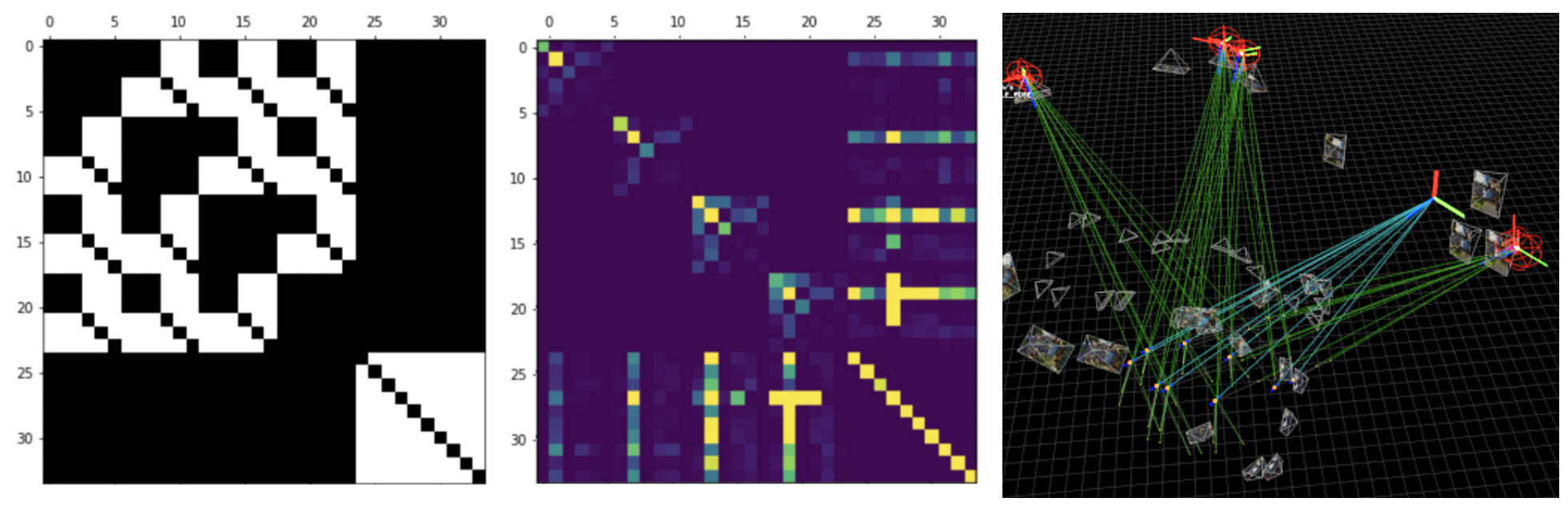
Over the past decade at Skydio, we’ve learned a lot about building autonomous robots at scale. Our first drone, the R1, was powered by a state-of-the-art motion planner that needed to balance dynamic flight, obstacle avoidance, and cinematography objectives in real-time. However, as our team continued to push the limits, we found it increasingly cumbersome to model complex aerodynamics and vision-based objectives within our system. About five years ago, we saw an opportunity to rethink our approach with symbolic computation and built the new motion planner that shipped with the Skydio 2. This motion planner was substantially more powerful at modeling complex objectives, required less code to maintain, and was able to run at higher rates on our drones.
SymForce was born when we realized that this same approach generalized well to many other areas of our system across computer vision, state estimation, and controls. It’s an incredible tool that allows our team to quickly progress from rapid prototyping to the type of highly-optimized runtime code that powers our drones. SymForce is the result of five years of development by Skydio’s autonomy team in an environment where performance and code maintainability are crucial. We think the challenges it solves are common and that SymForce can help robotics engineers build faster, the same way that PyTorch and TensorFlow accelerated the deep learning ecosystem.
SymForce is hosted at https://github.com/symforce-org/symforce . The accompanying paper is hosted at https://arxiv.org/abs/2204.07889 and has been accepted to RSS 2022.
What SymForce is
SymForce is a library written in Python and C++ that combines the development speed and flexibility of symbolic mathematics with the performance of auto-generated, highly optimized code. SymForce makes it possible to code a problem once, experiment with it symbolically, generate optimized code, and then run highly efficient optimization problems based on the original problem definition. This general-purpose workflow is effective for solving a wide variety of tasks in robotics and related domains, and can speed up common tasks by an order of magnitude while requiring less handwritten code and reducing the surface area for bugs.
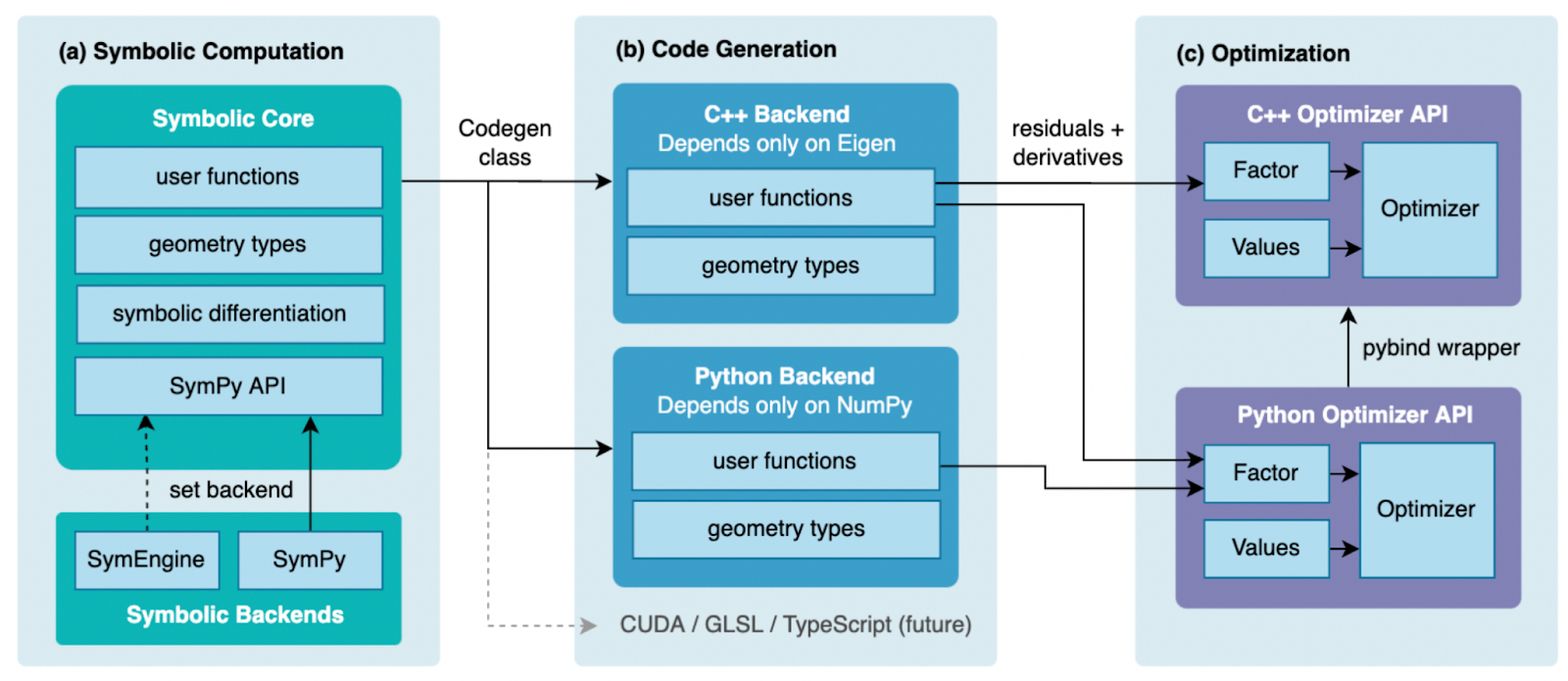
First, a problem is modeled with symbolic expressions in Python using the amazing SymPy library (and its C++ rewrite SymEngine). Symbolic math allows for more rapid understanding, debugging, and mathematical transformations over using numbers directly. SymForce adds components like 3D geometry types, camera models, noise models, and novel singularity handling techniques that make it possible to model complex robotics problems as symbolic expressions.
Second, functions on symbolic expressions are transformed into blazing-fast, branchless code for a chosen runtime language. Runtime functions maintain the same APIs as the symbolic functions, using runtime equivalents of the geometry and camera types. The runtime functions have minimal dependencies, which makes them useful even on embedded microcontrollers. It is easy to support new programming languages by creating a plugin.
Finally, runtime functions can be integrated as factors into the fast nonlinear optimization library within SymForce. The library is built for real-time robotics applications, with native support for optimizing geometric manifolds within a factor graph formulation. The library is written in C++, with Python bindings for experimentation.
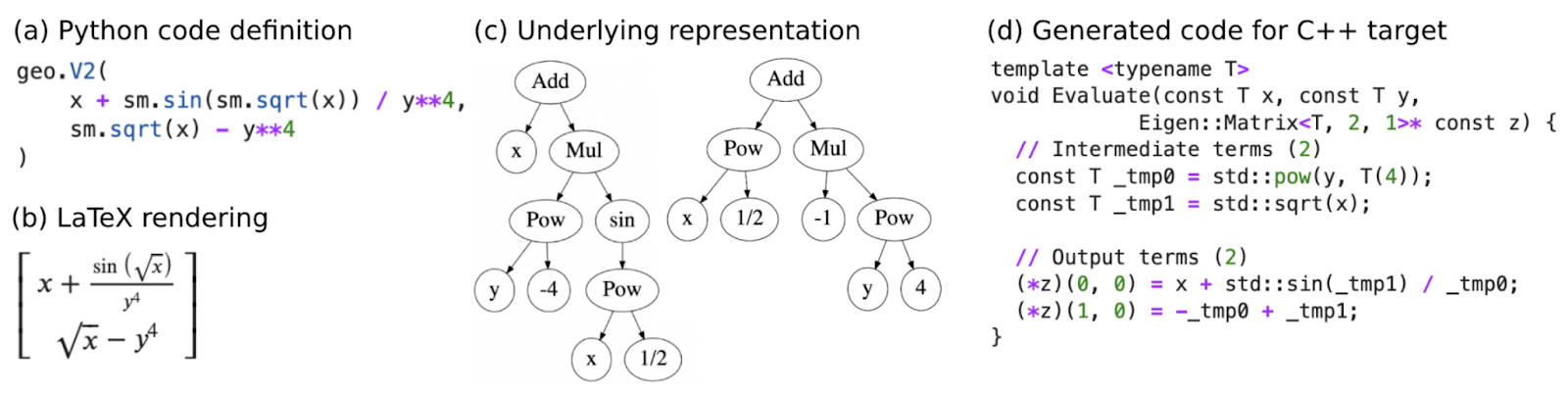
These components can be used independently or connected together in a seamless workflow. See the README tutorial for a full walkthrough of modeling a robot localization problem in Python, generating C++ code, and running a nonlinear optimizer.
Why SymForce is fast
SymForce can generate code that greatly outperforms standard approaches because it uses fine-grained knowledge of the structure of a computational task to avoid unnecessary work.
To see this in action, let’s take as an example the task of multiplying two (6, 6) matrices X and Y. While this example is basic, similar matrices are common in robotics, especially when dealing with 3D transformations.
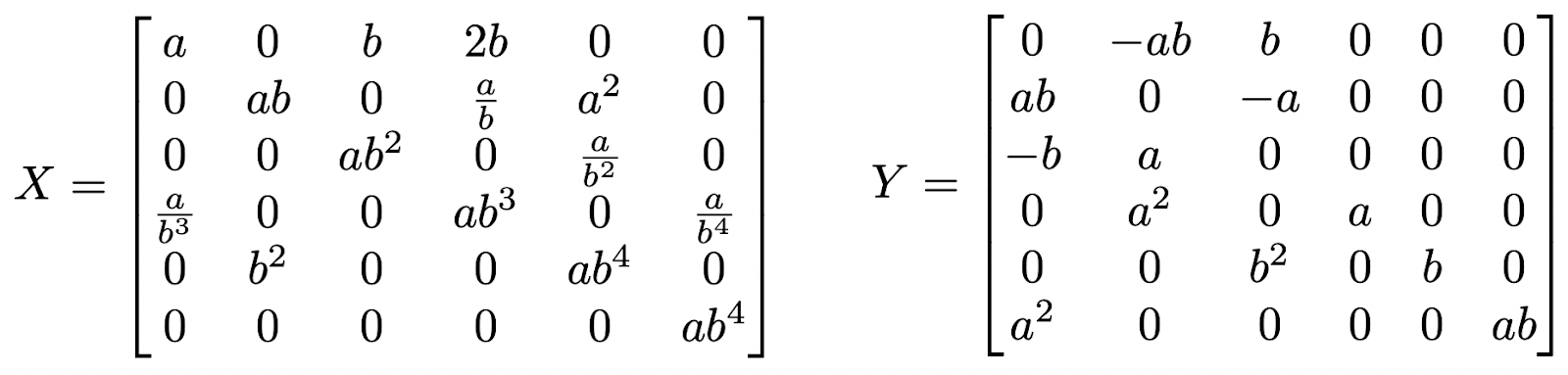
First, notice that there are repeated terms (also called common subexpressions) in the entries of X and Y. A compiler will try to avoid recomputing these expressions multiple times, but it can be hard to do so if X and Y are computed in separate functions. This presents a paradox because software engineers strive to organize code into small, composable functions to improve code quality. Symbolic math solves this with a complete separation between code structure and performance. The symbolic code is written with modular functions, but at runtime the entire expression is flattened into a single chain of instructions that share all common subexpressions.
Second, notice that X and Y are sparse. Most of the multiplications required to densely compute the product XY involve a zero entry and can be skipped entirely. There are many libraries for sparse matrix multiplication that do this, but they require dynamic memory allocation in a way that only leads to speedups for much larger matrix sizes. In SymForce, because X and Y are written in symbolic form, the generated function computes XY sparsely with no runtime overhead.
We can quantify these effects in terms of the number of scalar operations required. Dense multiplication of (N, N) matrices requires (N + (N − 1)) N*2 operations, so 396 for N = 6. Combined with 21 operations to compute the values within the matrices, it takes a total of 417 symbolic operations to compute XY . By multiplying matrices symbolically and generating code for the result, we both exploit the structure of the matrices and share expressions between them. XY can be computed in just 34 symbolic operations, a 12x reduction:
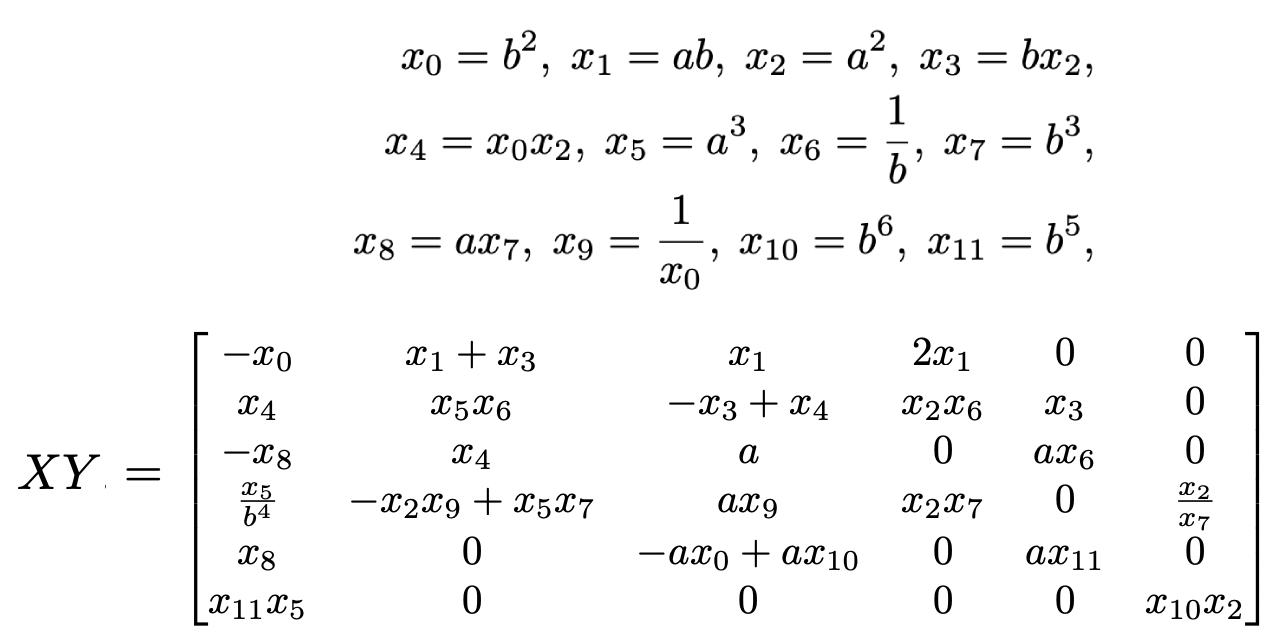
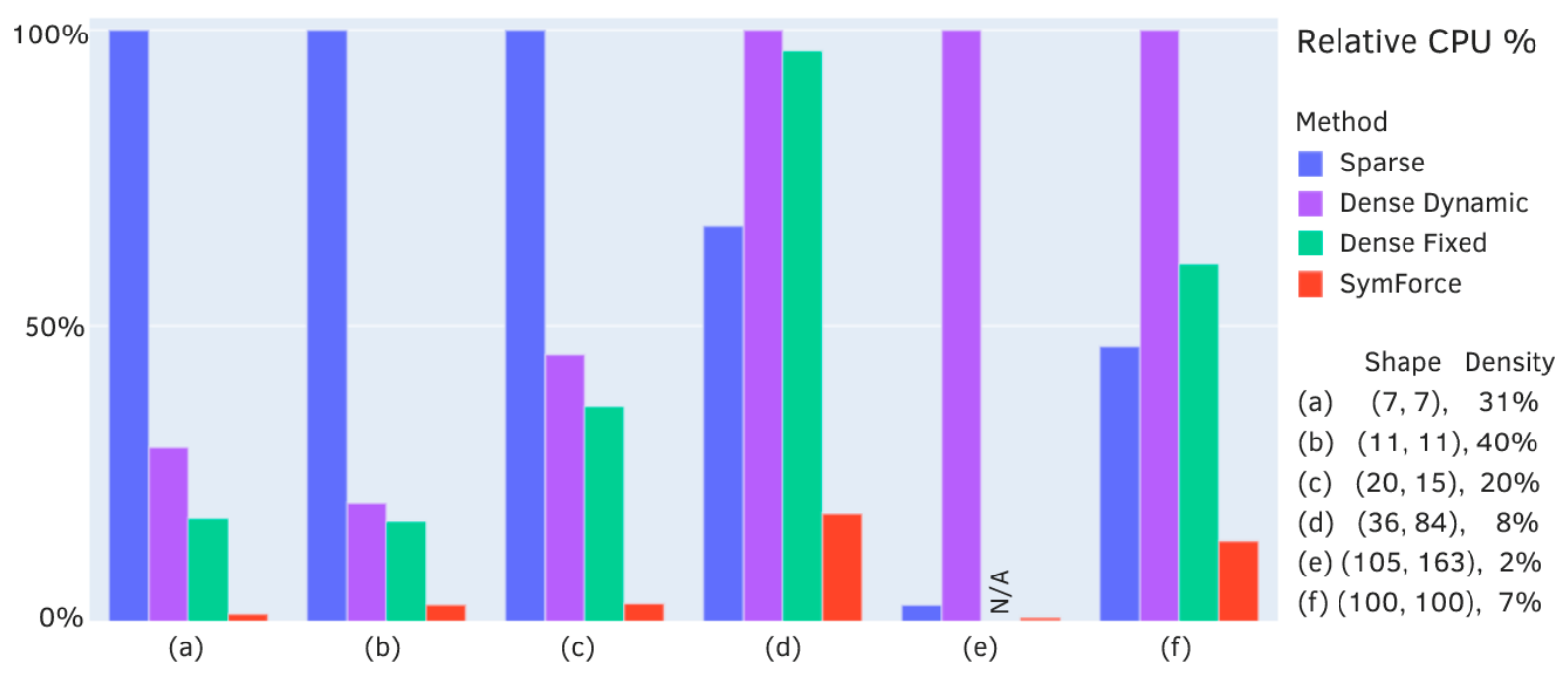
This demonstration is theoretical so far. The first experiment in the SymForce paper measures this task for a set of sparsity patterns from the SuiteSparse collection, varying from (7, 7) to (105, 163) in size. The entries of the matrices are randomly generated expressions, and we compare the flattened SymForce approach with dense and sparse implementations of the C++ Eigen library to demonstrate real-world gains.
SymForce outperforms the second best alternative by an average of 7.1x on an NVIDIA TX2 and 4.8x on an Intel CPU. SymForce is able to leverage sparsity and share common subexpressions with zero runtime overhead. Detailed profiling shows an order of magnitude reduction in the number of cache loads.
Beyond matrix multiplication, the second and third experiments in the paper show similar speedups in computing derivatives of 3D transformations and in solving a robot localization problem. At their core, robotics problems are composed of many operations that can be sped up with these techniques. The SymForce approach of flattening computation can yield even bigger wins on very complex expressions that are the result of more layers of computation.
Derivatives
One of the key advantages of SymForce is to dramatically improve the computation of derivatives. In robotics and many other fields, computing correct and efficient derivatives is one of the most critical development tasks. The standard approach is to hand-write derivatives for a core set of operations, and then rely on the chain rule to combine them together at runtime. This can be a large challenge and a common source of bugs, especially when dealing with complex geometric problems that need to be formulated with Lie groups.
SymForce introduces a novel method to automatically compute tangent space derivatives of functions that operate on Lie groups, avoiding all handwritten derivatives (and associated testing and maintenance). In addition, SymForce is able to flatten computation across entire expression graphs by sharing subexpressions and taking advantage of any available sparsity. As a result, SymForce derivatives can be significantly faster than alternatives that chain derivatives together at runtime. This combination of ease of use and speed is transformative in accelerating the time to robust solutions.

Into the world
We are incredibly excited to release SymForce to the open-source community. We think its core components can be useful in any domain that requires algorithmic code and can benefit a wide range of audiences from high-school students to tech companies. At Skydio, we developed it for real-time robotics algorithms like SLAM, calibration, bundle adjustment, MPC, and system identification.
While SymForce already powers tens of thousands of robots at Skydio, the public library is new and we are releasing it in beta stage. This is just the beginning, and we are excited for engagement from the community. If you are interested in joining our world-class Skydio team, contributing to SymForce is a fantastic way to meet us!
Code: https://github.com/symforce-org/symforce
Paper: https://arxiv.org/abs/2204.07889
Docs: https://symforce.org/






